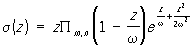
Сигма-функции, целые трансцендентные функции, введённые К. Вейерштрассом при построении им своей теории эллиптических функций. Основной из четырёх С.-ф. является функция

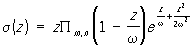
  где w = 2mw₁ + 2nw₂, w₁ и w₂ — два числа, отношение которых не является вещественным, а m и n независимо друг от друга пробегают все положительные и отрицательные целые числа, кроме m = n = 0. Функция s(z) имеет простые нули при z = w, т. е. в вершинах параллелограммов, образующих правильную решётку на плоскости z; эти параллелограммы получаются из основного параллелограмма с вершинами в точках 0, 2w₁, 2w₂, 2 (w₁ + w₂) параллельными переносами вдоль его сторон.

  При помощи функции s(z) могут быть определены дзета-функция x(z) и эллиптическая функция Ã(z) Вейерштрасса:

  , .

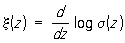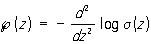  Обозначим w₃ = - w₁ - w₂, x(w_k) = h_k, k =1, 2, 3.

  Формулы

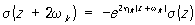  , k = 1, 2, выражают свойство квазипериодичности функции s(z). Равенства

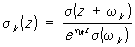  , k = 1, 2, 3,

  определяют остальные три С.-ф. Имеем s(0) = 0, s_k (0) = 1, k = 1, 2, 3. Функция s(z) является нечётной, а три остальные С.-ф. — чётные.

  Любая эллиптическая функция f (z) с периодами 2w₁ и 2w₂ может быть рационально выражена через С.-ф. по формуле

  ,

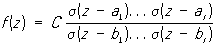  где С — постоянная, a₁,..., c_r и b₁,..., b_r — соответственно полные системы нулей и полюсов функции f (z), удовлетворяющие условию a₁ +... + a_r = b₁ +... + b_r.

  С.-ф. тесно связаны с тэта-функциями.

  Лит.: Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М., 1969; Гурвиц А., Курант Р., Теория функций, пер. [с нем.], М., 1968; Уиттекер Э. Т. и Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963.

Оглавление